突然ですが、球の表面積の公式は知っていますか?中学1年生が新しい公式を見つけた感動のお話です。
球の表面積の公式
普通は S = 4πr2 です。
これは一体何を表しているでしょうか。球の表面積(S)は、円の面積(πr2)の4倍とは?
高校数学(積分)を使った説明が正確ですが、中学生には直感的なイメージで理解しやすくすることも大切です。
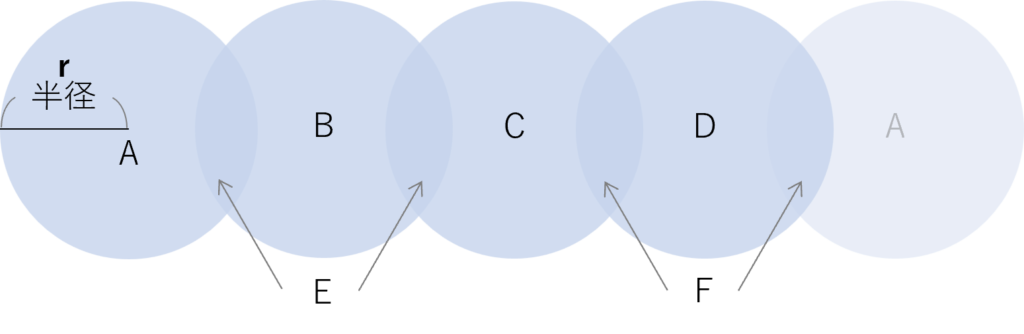
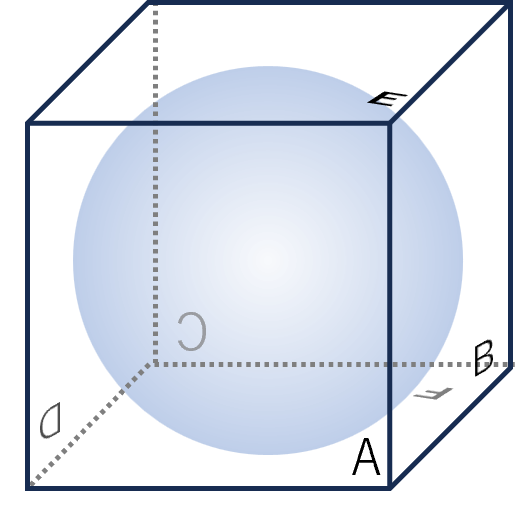
例えば、立方体にぴったりの球を入れたとき、各面(ABCD)から見える円の面積4つ分と等しくなります。だから「4」がつく。これくらいの説明のほうが「4」の意味がイメージしやすいのではないでしょうか。
新・球の表面積の公式
私が中1生に、復習のつもりで「球の表面積は?」と聞くと、こう答えました。
(生徒)「直径×直径×π・・・」
(私)「惜しい。半径だから・・・あ、え・・・合ってる・・・」
なんということでしょう。私は今まで、このような発想をしたことがありませんでした。感動です。
4πr2 = 2r × 2r × π
つまり
直径 × 直径 × π
なのです。
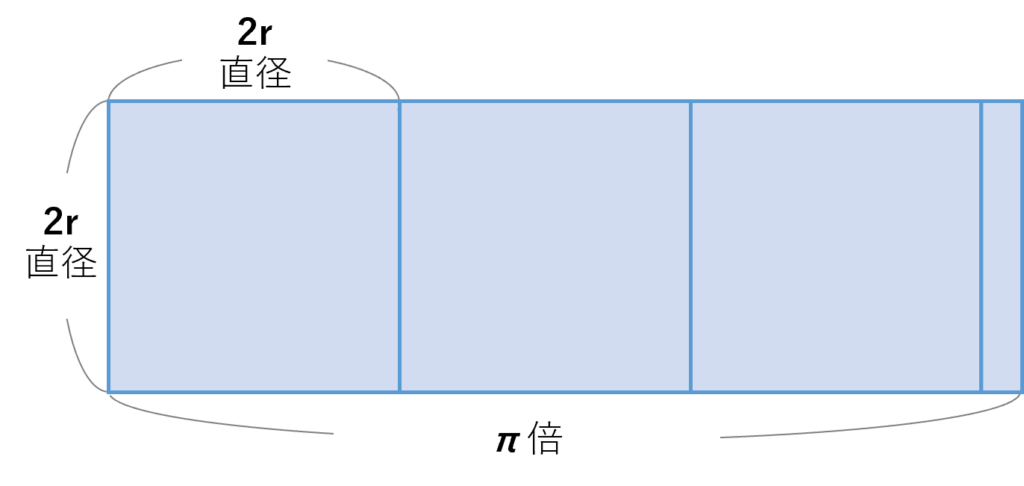
謎の「4」という数字を使わず、「直径×直径×円周率」と日本語だけで表すことができる美しい公式が誕生しました。
さらに広がった発見
この公式から、さらにおもしろい発見がありました。
- 横幅の「直径 × π」とは、円周の長さそのもの。
- 表面積は、球をピッタリ合わせた立方体の1つの面(2r×2r)のπ倍でもある。
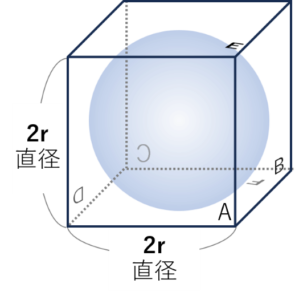
このように1つの発想から、いくつも見方が広がっていきます。
筑波塾の特長と理念
今回の出来事から、答えは1つでもそこにたどり着くまでの「わかりやすい考え方」はたくさんあることに、改めて気づかされました。
筑波塾は、一人ひとりに合わせた解法を指導するのが特長です。集団授業では、講師の説明だけでなく、生徒の考え方も積極的に共有します。「そんな考え方もあるんだ」と知ることで、自分に合った見方を見つけるきっかけが増えるからです。
今回の「直径 × 直径 × π」という公式も、まさに生徒の発想から生まれたものでした。教える側が用意した答えだけでなく、生徒自身の気づきや工夫を大切にすること。それが、理解を深め、学ぶ楽しさを育てると考えています。
「生涯学びを楽しみ、その成果を生かす」筑波塾の方針が、また一つ、実績として積み上がりました。
これからも一人ひとりの「わかった!」が生まれる瞬間を、これからも大切にしていきたいと思います。


